Gravitation explained

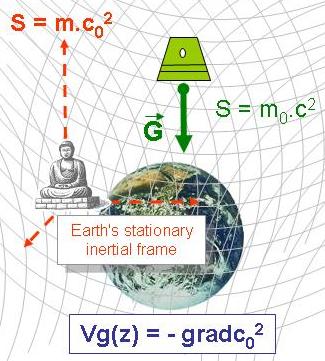
Gravitation acceleration yields no inertial force

It is a known fact of astronauts: when a space capsule free falls, its passengers float in weightlessness. This lack of force can be strangely regarded because the capsule is submitted to the constant acceleration of gravitation. Actually, any accelerated system at ground level yields an inertial force which is explained by synergetics in a previous article.

Whereas official physics explains how an existing inertia is directly nullified by the weight, STEM-Physics, which primarily considers the interacting energies, relates this lack of force to a constant synergy.
Consequently the synergy of the capsule remains constant so that:

• dS/dt = m₀ .dc² /dt = 0 (1)

Gravitation explained - Demonstration 1

The relationship (2) between the internal speed of light c and the external one c₀ comes out from the expression of kinetic energy already explained there. Unlike special relativity does, it is unnecessary to consider neither uniform motions nor constant speeds in order to obtain expression (2). It is therefore fairly applicable in the case of the capsule submitted to gravitation.

• according γ = (1 - v² /c₀ ² )^-1/2

• c² = γ.c₀ ² (2)

• so (1) and (2) imply: d(γ.c₀ ² )/dt = 0 (3)

The external speed of light c₀ can't be a constant because it would make expression (3) impossible to resolve. Thus (3) becomes:

• c₀ ² .dγ/dt + γ.dc₀ ² /dt = 0 (4)

• which infers (v.dv/dt + (2.c₀ - 3.v² /c₀ ).dc₀ /dt) = 0 (5)

In the obvious case where v << c₀ , expression (5) provides the amazing formula in (6):

• dv/dt = -1/v.dc₀ ² /dt = -dc₀ ² /dz (6)

The acceleration of the capsule, it is to say the acceleration of gravitation, equals the variation of the squared speed of light along space coordinates.
In conclusion, acceleration of gravitation occurs owing to the speed of light that decreases around masses.

• V_g = - gradc₀ ²

Gravitation explained - Demonstration 2

A more straightforward demonstration is to consider the same object at two different heigths. Passing from the higher state to the lower corresponds to a loss of potential energy known as:

• ΔE_field = m₀ .V_g .Δh

Because free falling from the higher point to the lower yields no inertia, it can be deduced that synergy between the two states doesn't change:

• ΔS = m₀ .Δc₀ ² + ΔE_field = 0

• consequently m₀ .Δc₀ ² = - m₀ .V_g .Δh

• and V_g = - Δc₀ ² /Δh

How much does the speed of light vary?

According the value of gravitation acceleration on earth (roughly 10 m/s² ), and taking into account the difference of synergy between the ground and the top of the Eiffel Tower in Paris (roughly 300 m height), a difference of c₀ ² is:

• Δc₀ ² = - 3,000 (m/s)²

• also 2.c₀ .Δc₀ = - 3,000 (m/s)²

• However, because of the huge value of the speed of light (3 10⁺⁸ m/s), a very few and non measurable difference of speed provides gravitation: Δc₀ = - 0.5. 10^-5 m/s along a 300 meters height

Amazingly, the gross of gravitation comes out from a tiny variation of the speed of light.

At a conclusion, we can understand how official physics is at the same time right and wrong when considering the speed of light as a constant: right because the speed of light actually varies so few, wrong because the consequences of this variation can't be neglected in most of formulas.