The Physical Fields as specific properties of Space

Physical fields and their properties

Since Newtown brought up a correct model for forces of gravity, other physical phenomena have been identified to operate throughout empty space along particular lines of stress.
To be more precise, only three similar phenomena are identified up to now:

• The Gravity forces

• The Electrostatics forces

• The Magnetostatics forces

All three share identical properties:

• They operate everywhere in space along lines of stress

• Their strength follows a law inversely proportionnal to a squared distance

• A particular coefficient characterizes the interaction between their force and matter: the mass for Gravitation, the charge for Electrostatics and the magnetic mass or the magnet strength for Magnetostatics

• They transform kinetic energy from and into a weird and unexplained potential energy

• Every perturbation of these fields apparently propagate at the speed of light

To best describe these forces, the notion of physical field has been introduced: a physical quantity specified at points throughout space.

It is then obvious that physical fields, and therefore the forces that are generated from them, are specific properties of a Space Medium.

The potential Energy

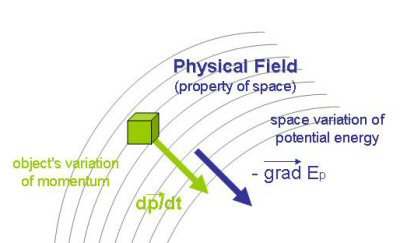
When a material object is left into a field, it can be attracted or repelled due to the force of that field. According the primary law of dynamics, that force corresponds to a momentum derivative (1). Additionaly the work of this force represents a loss of the potential energy managed by the field (2) which is transformed into kinetic energy.

• dp/dt = F (1)

• F.dl = dE (2)

From (1) and (2) comes the obvious relationship between energy and momentum: F.dl = dp/dt.dl = dE. Since dl = v.dt, there can be inferred that:

• dp.v = dE (3)

Moreover, the operating force represents a loss or a gain of a potential energy. This weird energy that only depends on the position of the object in the field can suggest that it is due to a gradient of the field's potential energy. Thus (2) can more fairly be expressed as:

• F = - gradE_p (2')

From which another version of equation (3) is a conservative one:

• dp/dt + gradE_p = 0 (3')

The expression (3') clearly brings a relationship between the dynamics of an object and a surrounding field. Admitting that any physical field characterizes the properties of a space medium implies first that material objects constantly interact with its surrounding space in a field.

Next...